「テストの勉強時間が増えると、成績は本当に上がるの?」
「身長が高い人ほど、足のサイズも大きい?」
こんな疑問をデータで確かめるのが回帰分析です!
回帰分析を使うと、2つのデータの関係を数式で表すことができ、未来の予測にも役立ちます。統計って難しそうに思えるかもしれませんが、身近なことに応用できると、意外と面白いんです!
本記事では、散布図と回帰分析の基本をわかりやすく解説します!数学が苦手な人でも大丈夫!データを読み解くコツを一緒に学んでいきましょう!
- 散布図と回帰分析について知りたい方
- 学生にもわかりやすい解説を求めている方
- ITパスポートの勉強をしている方
散布図とは
散布図とは、2つのデータの関係をわかりやすくするグラフです。横軸(X軸)に1つのデータ、縦軸(Y軸)に1つのデータを置いて、点を打ちます。
例えば、学校の「勉強時間(X軸)」と「テストの点数(Y軸)」を散布図にすると、こんな感じになります。このグラフを見る感じ、勉強時間が長いほどテストの点数も高くなっていってることが分かりますね。
散布図はこのようにぱっと見で、2つのデータの関係を見ることができます!
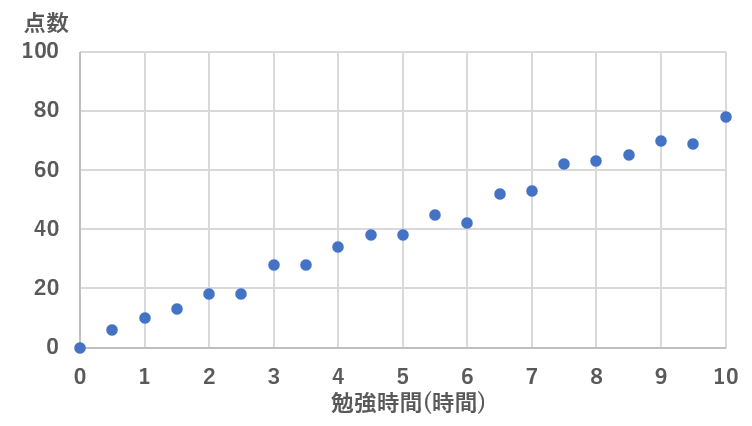
また、2つデータがどのような関係かを「正の相関」「負の相関」「無相関」といった言葉で表します。
- 右肩上がりのグラフ:正の相関(例:勉強時間とテストの点数は正の相関)
- 右肩下がりのグラフ:負の相関(例:勉強時間とゲームの時間は負の相関)
- バラバラのグラフ:無相関(例:勉強時間と身長は無相関)

正の相関
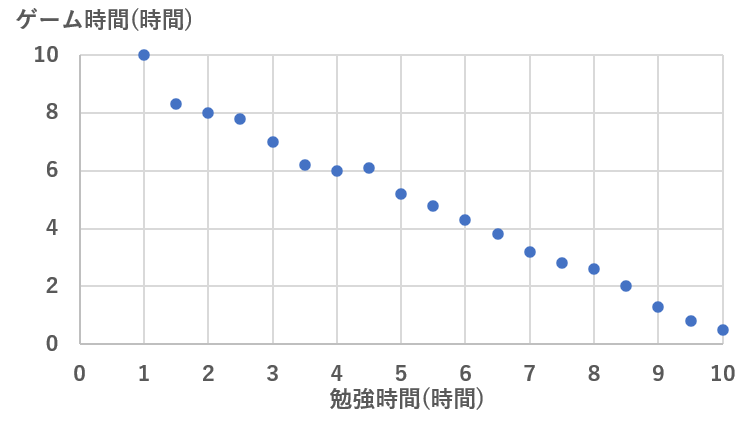
負の相関
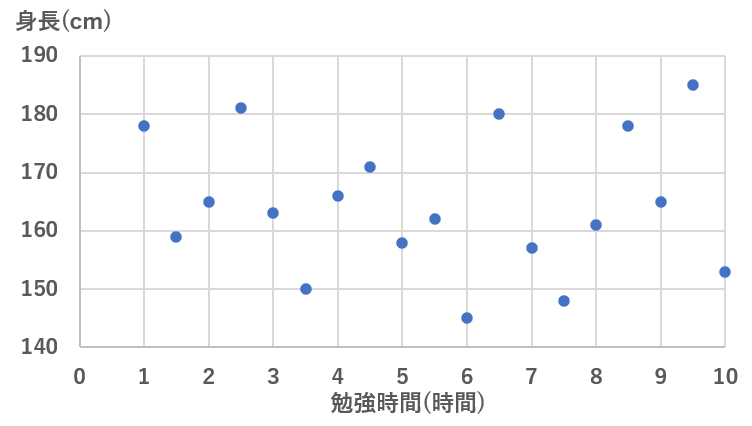
無相関
回帰分析とは
回帰分析は、データの関係性を数式で表し、未来の予測や傾向を分析する手法です。
散布図だけでもぱっと見で2つのデータの関係がわかりますが、回帰分析は具体的な数値(数式)で表します!
例えば、「広告費が売上にどれくらい影響を与えているか?」や「気温がアイスの売上にどう関係するのか?」を分析するのに役立ちます!
ただ100%その結果になるわけではないので注意が必要です。
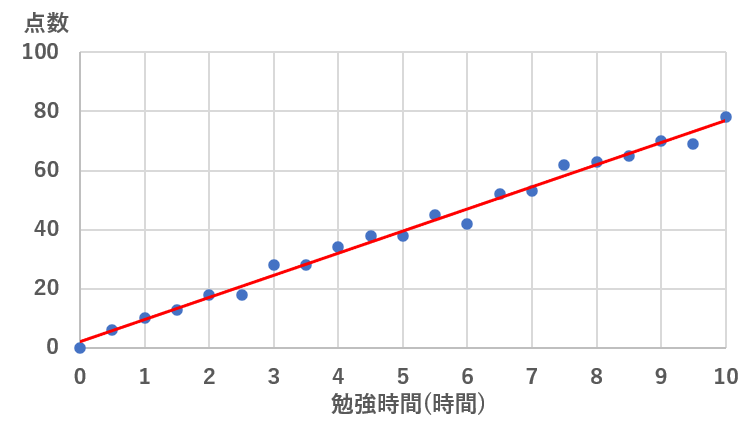
回帰分析にはいろいろな種類があります。
先ほどの「勉強時間とテストの点数」の例は単回帰分析になります。
- 単回帰分析:2つのデータの関係を分析(例:勉強時間とテストの点数は関係しているか)
- 重回帰分析:ある1つの事象と2つ以上の要因の関係を分析(例:テストの点数は「勉強時間」と「睡眠時間」が関係しているか)
- ロジスティクス回帰分析:Yes/Noなどの2つに分類を行う分析手法(例:勉強を何時間以上すれば受験に合格できるか)
どんなところで回帰分析が使われているか
回帰分析は、いろいろなところで使われています。
- 不動産価格の予想
不動産会社や投資家は、地域、建物の広さ、築年数などの特徴を使って不動産の価格を予測するために回帰分析を使用します。

- マーケティング効果の分析
企業が広告予算やキャンペーンの効果を評価する際に回帰分析を使用します。例えば、テレビ広告の費用が売上にどのくらい影響を与えるかを分析します。

- 医療分野での治療効果の評価
医学の研究では、治療法や薬が患者の健康にどのように影響を与えるかを回帰分析で調べることがあります。例えば、新薬の服用量と血圧の変化との関係を調べる場合です。
まとめ
散布図とは、2つのデータの関係をわかりやすくするグラフです。
回帰分析は、データの関係性を数式で表し、未来の予測や傾向を分析する手法です。
散布図と回帰分析を活用することで、データ同士の関係と将来どうなるか予測をたてられます!
勉強や日常生活の中で、ぜひ散布図を活用してみましょう!



